


Next: Context free grammars
Up: Showing that a language
Previous: The pumping lemma
Applying the pumping lemma
Theorem 4.2
The language
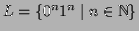
is not regular.
Proof:
Assume  would be regular. We will show that this leads to
contradiction using the pumping lemma.
would be regular. We will show that this leads to
contradiction using the pumping lemma.
Now by the pumping lemma there is an 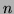 such that we can split each
word which is longer than
such that we can split each
word which is longer than 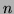 such that the properties given by the
pumping lemma hold. Consider
such that the properties given by the
pumping lemma hold. Consider
 , this is certainly longer
than
, this is certainly longer
than 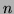 . We have that
. We have that
 and we know that
and we know that
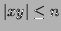 ,
hence
,
hence  can only contain as, and since
can only contain as, and since
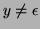 it must
contain at least one a. Now according to the pumping lemma
it must
contain at least one a. Now according to the pumping lemma
 but this cannot be the case because it contains at least one a
less but the same number of bs as
but this cannot be the case because it contains at least one a
less but the same number of bs as  .
.
Hence, our assumption that  is regular must have been wrong.
is regular must have been wrong.

It is easy to see that the language
is regular (just construct the appropriate DFA or use a regualr
expression). However what about
where by saying  is a square we mean that is there is an
is a square we mean that is there is an
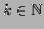 s.t.
s.t.  . We may try as we like there is no way to find out
whether we have a got a square number of
. We may try as we like there is no way to find out
whether we have a got a square number of  s by only using finite
memory. And indeed:
s by only using finite
memory. And indeed:
Theorem 4.3
The language
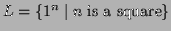
is not regular.
Proof:
We apply the same strategy as above. Assume  is regular then there
is a number
is regular then there
is a number 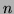 such we can split all longer words according to the
pumping lemma. Let's take
such we can split all longer words according to the
pumping lemma. Let's take  this is certainly long enough. By the
pumping lemma we know that we can split
this is certainly long enough. By the
pumping lemma we know that we can split 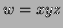 s.t. the conditions of
the pumping lemma hold. In particular we know that
s.t. the conditions of
the pumping lemma hold. In particular we know that
Using the 3rd condition we know that
that is  is a square. However we know that
is a square. However we know that
To summarize we have
That is  lies between two subsequent squares. But then it
cannot be a square itself, and hence we have a contradiction to
lies between two subsequent squares. But then it
cannot be a square itself, and hence we have a contradiction to
 .
.
We conclude  is not regular.
is not regular.

Given a word
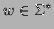 we write
we write  for the word read backwards. I.e.
for the word read backwards. I.e.
 . Formally this can be defined as
. Formally this can be defined as
We use this to define the langauge of even length palindromes
I.e. for
 we have
we have
 .
Using the intuition that finite automata can only use finite memory it
should be clear that this language is not regular, becasue one has to
remember the first half of the word to check whetherthe 2nd half is
the same word read backwards. Indeed, we can show:
.
Using the intuition that finite automata can only use finite memory it
should be clear that this language is not regular, becasue one has to
remember the first half of the word to check whetherthe 2nd half is
the same word read backwards. Indeed, we can show:
Theorem 4.4
Given
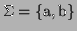
we have that
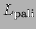
is not regular.
Proof: We use the pumping lemma: We assume that
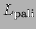 is regular. Now given a pumping number
is regular. Now given a pumping number 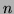 we construct
we construct
 , this word is certainly longer than
, this word is certainly longer than
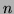 . From the pumping lemma we know that there is a splitting of the
word
. From the pumping lemma we know that there is a splitting of the
word 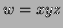 s.t.
s.t.
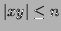 and hence
and hence  may only contain 0s and
since
may only contain 0s and
since
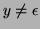 at least one. We conclude that
at least one. We conclude that
 where
where
 where
where  . However,
this word cannot be a palindrome since only the first half conatains
any
. However,
this word cannot be a palindrome since only the first half conatains
any  s.
s.
Hencce our assumption
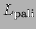 is regular must be wrong.
is regular must be wrong.

The proof works for any alphabet with at least 2 different
symbols. However, if  contains only one symbol as in
contains only one symbol as in
 then
then
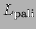 is the laguage of an even
number of
is the laguage of an even
number of  s and this is regular
s and this is regular
 .
.



Next: Context free grammars
Up: Showing that a language
Previous: The pumping lemma
Thorsten Altenkirch
2001-05-08
![]() would be regular. We will show that this leads to
contradiction using the pumping lemma.
would be regular. We will show that this leads to
contradiction using the pumping lemma.
![]() such that we can split each
word which is longer than
such that we can split each
word which is longer than ![]() such that the properties given by the
pumping lemma hold. Consider
such that the properties given by the
pumping lemma hold. Consider
![]() , this is certainly longer
than
, this is certainly longer
than ![]() . We have that
. We have that
![]() and we know that
and we know that
![]() ,
hence
,
hence ![]() can only contain as, and since
can only contain as, and since
![]() it must
contain at least one a. Now according to the pumping lemma
it must
contain at least one a. Now according to the pumping lemma
![]() but this cannot be the case because it contains at least one a
less but the same number of bs as
but this cannot be the case because it contains at least one a
less but the same number of bs as ![]() .
.
![]() is regular must have been wrong.
is regular must have been wrong.
![]()
![]() is regular then there
is a number
is regular then there
is a number ![]() such we can split all longer words according to the
pumping lemma. Let's take
such we can split all longer words according to the
pumping lemma. Let's take ![]() this is certainly long enough. By the
pumping lemma we know that we can split
this is certainly long enough. By the
pumping lemma we know that we can split ![]() s.t. the conditions of
the pumping lemma hold. In particular we know that
s.t. the conditions of
the pumping lemma hold. In particular we know that
![]() is not regular.
is not regular.
![]()
![]() we write
we write ![]() for the word read backwards. I.e.
for the word read backwards. I.e.
![]() . Formally this can be defined as
. Formally this can be defined as
![]() is regular must be wrong.
is regular must be wrong.
![]()
![]() contains only one symbol as in
contains only one symbol as in
![]() then
then
![]() is the laguage of an even
number of
is the laguage of an even
number of ![]() s and this is regular
s and this is regular
![]() .
.